
Figure 1
La résonance stochastique
ou la transmission non
linéaire du signal favorisée par le bruit
Xavier Godivier, François Chapeau-Blondeau
Laboratoire d'Ingénierie
des Systèmes Automatisés, Faculté des Sciences, Université
d'Angers,
2 boulevard Lavoisier, 49000
ANGERS, FRANCE.
Résumé
:
Le phénomène
de résonance stochastique est un effet non linéaire dans
lequel le bruit est capable de favoriser la transmission d'un signal utile.
Cet effet peut revêtir diverses formes, selon les types considérés
pour le bruit, le signal utile, le système non linéaire de
transmission, et la mesure de performance qui se voit améliorée
par ajout de bruit. Nous présentons ici de manière synthétique
ce phénomène, en insistant sur les résultats récents
auxquels nous avons contribué.
(Remarque: les références seront ajoutées ultérieurement)
Introduction
La résonance stochastique est un phénomène par lequel la transmission d'un signal utile ou cohérent, par certains systèmes non linéaires, peut être améliorée par l'augmentation du bruit appliqué au système .
Cet effet non linéaire paradoxal a originellement été introduit, il y a une quinzaine d'années, dans le contexte de la dynamique des climats, afin d'expliquer la récurrence régulière des ères glaciaires. La survenue des ères glacières résulte d'une interaction non linéaire entre une cause périodique due aux mouvements planétaires (signal cohérent) et une cause aléatoire due aux perturbations atmosphériques et climatiques (bruit), et pour lesquelles il apparaît que l'influence, sur le résultat, de la cause cohérente périodique peut être renforcée en augmentant la cause aléatoire.
Depuis ce point de départ, l'étude de la résonance stochastique s'est d'abord développée pour le cas de la transmission d'un signal périodique par certains systèmes dynamiques non linéaires bistables. Progressivement, le phénomène a été mis en évidence dans différents systèmes de ce type, incluant des circuits électroniques , des lasers, la résonance paramagnétique électronique , des neurones, des composants supraconducteurs.
Depuis peu, le phénomène de résonance stochastique a été étendu à une classe beaucoup plus large de systèmes non linéaires, qui réalisent la transmission de signaux utiles périodiques ou apériodiques. Également, le cadre de définition de la résonance stochastique a été élargi, en montrant les liens avec d'autres situations où le bruit peut favoriser le signal utile, comme le "dithering noise'' utilisé lors de la conversion analogique-numérique d'un signal ou dans le codage d'une image. Aujourd'hui, la résonance stochastique apparaît comme un phénomène non linéaire général, observable dans de nombreux systèmes, et qui désigne un effet de transmission du signal favorisée par le bruit, pouvant revêtir diverses formes selon les types considérés pour le bruit, le signal utile, le système non linéaire de transmission, et la mesure de performance qui peut être améliorée par ajout de bruit.
Dans cet article, nous décrirons
d'abord brièvement le phénomène de résonance
stochastique dans la forme primitive où il fut originellement introduit,
pour la transmission d'un signal périodique par un système
dynamique non linéaire bistable. Nous présenterons ensuite
nos propres travaux, qui concernent l'extension de la résonance
stochastique périodique à une classe générale
de systèmes dynamiques non linéaires, ainsi que l'extension
aux signaux apériodiques. Nous présenterons enfin nos résultats
concernant l'étude de la résonance stochastique dans des
systèmes naturels réalisant du traitement non linéaire
du signal très performant : les systèmes neuronaux.
1 Système dynamique non linéaire bistable
On considère le mouvement d'une particule dans un système gouverné par une dynamique à potentiel bistable, tel que le potentiel quartique (Fig. 1)
|
(1) |

Figure 1
Le système est soumis à une excitation périodique s(t) = A sin(wt) et à un bruit h(t) d'amplitude rms s2
|
(2) |
En présence d'une excitation périodique seule et d'amplitude trop faible la particule ne peut pas franchir la barrière de potentiel situé à l'origine. Elle oscille alors périodiquement en restant confinée autours d'un des deux minima du potentiel. Si on ajoute un bruit h(t) celui-ci va permettre occasionellement à la particule de franchir la barrière de potentiel. Il en résulte alors en sortie un signal constitué de la succession des transition entre les deux puits du potentiel. Ce signal présente plus ou moins de corrélation avec le signal périodique en entrée s(t) suivant l'amplitude du bruit. Pour un faible niveau de bruit on obtient très peu d'activité en sortie. En augmentant l'amplitude du bruit on augmente alors l'effet de coopération du bruit avec le signal, ce qui se traduit par une plus grande corrélation du signal en sortie avec le signal s(t) en entrée. Cette augmentation se poursuit jusqu'à un niveau optimum du bruit. Puis au delà de ce niveau, la corrélation entrée-sortie diminue car le bruit devient prépondérant par rapport au signal s(t).
Dans le cas présent le signal d'entrée étant périodique, on peut évaluer l'efficacité du système à transmettre le signal s(t) en observant le spectre des fréquences. Celui-ci présente une succession de pics décroissant aux fréquences multiples entiers de la fréquence du signal périodique s(t) (Fig.2).
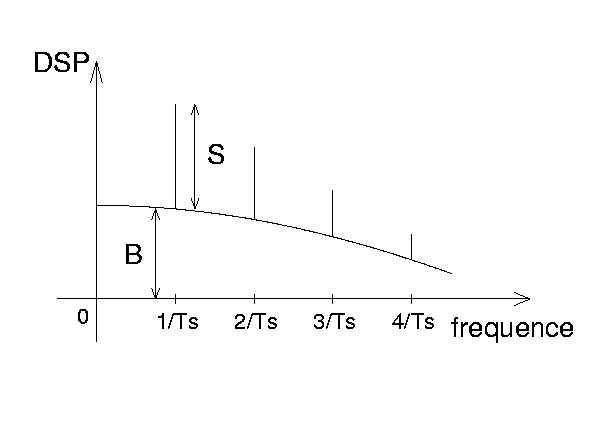
Figure 2
On peut définir alors un rapport signal sur bruit à partir du spectre des fréquences comme le rapport de la puissance contenue dans la raie spectrale en 1/Ts sur l'amplitude du fond de bruit qui l'entoure :
|
(3) |
On obtient ainsi une courbe
du rapport signal sur bruit en fonction de l'amplitude du bruit. Cette
courbe qui montre une augmentation puis une diminution du rapport signal
sur bruit est caractéristique du phénomène de résonance
stochastique.
2 Extension de la résonance stochastique périodique
Nous avons développé une théorie de la résonance stochastique pour les systèmes dynamiques non linéaires formés par l'association d'une non-linéarité statique en cascade avec un système dynamique linéaire quelconque . La résonance stochastique est un effet essentiellement non linéaire, et nous avons montré qu'il est suffisant de la caractériser dans la transmission de la non-linéarité statique. Nous allons présenter ici brièvement le cas de la résonance stochastique en présence d'un bruit blanc.
Considérons s(t) un signal cohérent périodique de période Ts, et h(t) un bruit blanc stationnaire de densité de probabilité fh(u). Ces deux signaux sont appliqués à l'entrée d'un système non linéaire statique délivrant la sortie
|
(4) |
En général, à cause de l'influence de l'entrée aléatoire h(t), la sortie y(t) est un signal aléatoire. Toutefois, ce signal aléatoire y(t) contient une part de corrélation avec l'entrée périodique s(t). Pour certaines fonctions g, cette part de corrélation de la sortie avec l'entrée cohérente, peut être augmentée en augmentant le bruit, ce qui est la manifestation de la résonance stochastique.
On montre que la part cohérente dans le signal de sortie y(t), se manifeste dans la densité spectrale de puissance de sortie Pyy(n), par des raies (pics de Dirac) aux multiples entiers de la fréquence cohérente 1/Ts. La puissance contenue dans la raie spectrale cohérente à la fréquence n/Ts est donnée par |[`Y]n|2, où
|
(5) |
|
(6) |
La sortie y(t) contient également des fluctuations aléatoires large-bande formant un fond continu dans la DSP Pyy(n) d'où émergent les raies cohérentes. Dans le cas d'un bruit blanc en entrée, ce fond continu dans la DSP de sortie Pyy(n) possède un niveau constant mesuré par la variance moyennée
|
(7) |
|
(8) |
On définit alors un rapport signal sur bruit (RSB) en sortie
|
(9) |
Grâce aux Eqs. (5)-(9), il est possible de calculer le RSB en présence d'une non-linéarité g, d'une entrée périodique s(t) et d'une distribution du bruit, toutes trois quelconques. On peut ainsi mettre en évidence des situations où le RSB augmente lorsque le niveau du bruit d'entrée augmente, ce qui est la signature de la résonance stochastique.
Pour une illustration simple, nous considérons la non-linéarité d'un comparateur à seuil Vth à deux états de sortie ±Vsat :
|
(10) |
Fig. 3 ( manquante
ici) : Rapport signal sur bruit en sortie Â,
en fonction de l'amplitude efficace s
du bruit d'entrée, pour la non-linéarité de l'Eq.
(10). Le trait plein est l'expression théorique
de l'Eq. (9), les jeux de valeurs discrètes sont
les mesures expérimentales de Â
sur une réalisation à amplificateur opérationnel du
comparateur, (*) à 1/Ts, (°)
à 2/Ts et (+) à 3/Ts.
Dans le cas de la Fig. 1, le signal cohérent s(t) est subliminal, c'est-à-dire qu'à lui seul il est incapable d'induire des transitions en sortie car son amplitude VM est inférieure au seuil Vth. Le RSB en sortie est alors strictement nul en l'absence du bruit. Dès que l'on commence à ajouter un peu de bruit gaussien, le signal cohérent devient visible en sortie, car le bruit et le signal coopèrent pour vaincre le seuil. Dans une première phase, plus on augmente le bruit en entrée et plus le signal cohérent est visible en sortie. Le RSB croît alors avec l'amplitude efficace s du bruit, et ce jusqu'à un niveau de bruit optimal où le RSB passe par un maximum. Au delà, le bruit domine dans la sortie et fait décroître le RSB.
La réf. montre le phénomène de résonance stochastique dans d'autres situations, par exemple avec des non-linéarités statiques continues non monotones comme g(u) = exp[-(u-q)2/l2] là où le signal cohérent n'est plus subliminal (voir aussi).
On peut noter également que d'autres mesures existent pour l'efficacité de la transmission qui est augmentée par le bruit, comme l'amplitude de la composante cohérente en sortie, une intercorrélation entre la sortie et l'entrée cohérente, ou des gains entrée-sortie montrant qu'il est possible non seulement d'augmenter le RSB en sortie en ajoutant du bruit mais également de rendre le RSB en sortie supérieur au RSB en entrée (voir aussi).
Enfin soulignons que dans la résonance stochastique périodique, le signal cohérent périodique peut en principe être considéré comme une porteuse haute-fréquence, qu'il serait possible de moduler au moyen d'un message basse-fréquence, le signal utile modulé pouvant alors profiter de la transmission assistée par le bruit comme elle est décrite ici.
La résonance stochastique
peut aussi être détectée dans la transmission d'un
signal cohérent apériodique large-bande, comme nous allons
le présenter maintenant.
3 Résonance stochastique apériodique
La résonance stochastique dans la transmission d'un signal apériodique large-bande n'a été mise en évidence que récemment, dans un modèle de neurone où elle est quantifiée au moyen d'une mesure de corrélation dont on peut augmenter la valeur en augmentant le bruit. a montré la possibilité de résonance stochastique dans un canal binaire en présence de bruit gaussien avec une mesure qui est une information mutuelle entrée-sortie au sens de Shannon, et en présence d'un bruit de distribution arbitraire avec une capacité informationnelle entrée-sortie. Pour illustrer l'effet, nous considérons ici un autre type de canal de transmission de l'information, pour lequel nous évaluons la capacité informationnelle et montrons qu'elle peut être augmentée en augmentant le bruit.
Nous considérons la transmission d'information par un canal sans mémoire. L'entrée du canal est une variable aléatoire discrète X qui peut prendre la valeur 1 ou -1 avec les probabilités respectives p1 et p-1 = 1-p1. La transmission sur le canal met en jeu deux effets. D'abord un bruit N est ajouté à l'entrée X pour fournir X+N. Ensuite, X+N est comparé à un double seuil fixe q > 0 pour déterminer la sortie discrète Y du canal selon :
|
|||||||||||||||||||
Le bruit N est une variable aléatoire continue de fonction de répartition F(u) = Pr{N £ u}. Les réalisations successives de l'entrée aléatoire X sont indépendantes et identiquement distribuées, et de même pour le bruit N. L'entrée X et le bruit N sont statistiquement indépendants.
Le canal en présence peut être considéré comme un canal binaire bruité avec effacement, où l'information binaire d'entrée X = ±1 peut être reçue par Y = ±1 de façon éventuellement éronnée, ou bien effacée quand Y = 0.
Pour les probabilités de transfert entrée-sortie de ce canal nous avons, par exemple, la probabilité p1,-1 = Pr{Y = 1 | X = -1} qui est aussi Pr{X+N > q| X = -1} valant Pr{N > q+1} = 1-F(q+1). Par des raisonnements similaires, on arrive a :
|
|||||||||||||||||||||||||||||||||||||||
Une fois connues les probabilités de transfert, l'information transmise I(X; Y) par le canal peut s'évaluer à partir des entropies comme :
|
(18) |
|
(19) |
|
(20) |
Les Eqs. (18)-(20) conduisent à une expression explicite de l'information transmise I(X; Y) en fonction des probabilités de transfert et de la probabilité d'entrée p1. Dans le cas où le bruit N est symétrique centré, c'est-à-dire de densité de probabilité paire, le processus de transmission d'information est symétrique, et l'information transmise est invariante dans l'échange des valeurs de p1 et p-1 = 1-p1. Comme l'information transmise par un canal discret sans mémoire est toujours une fonction convexe de la distribution de probabilité d'entrée, nous déduisons que pour N symétrique centré, le maximum de I(X; Y) qui définit la capacité informationnelle C du canal, est atteint pour p1 = 0.5 = p-1. Dans le cas d'un bruit symétrique centré, les Eqs. (18)-(20) avec p1 = 0.5, permettent donc d'évaluer explicitement la capacité C du canal de transmission, et d'étudier son évolution en fonction des propriétés statistiques du bruit N.
Pour fixer les idées, nous considérons un bruit N gaussien centré et nous examinons la variation de la capacité informationnelle C en fonction de l'amplitude efficace s = Ö{E(N2)} du bruit. La Fig. 2 représente cette variation pour différentes valeurs du seuil q. Les courbes de la Fig. 2 montrent clairement l'existence de deux régimes de fonctionnement distincts pour le canal. Quand q < 1, une entrée X = 1 (respectivement X = -1) est à elle seule suffisante pour déclencher une sortie Y = 1 (respectivement Y = -1). En l'absence du bruit, la capacité du canal est alors C = 1 bit. L'ajout du bruit N sera ici seulement ressenti comme une dégradation de la transmission, et ainsi la capacité C décroît à partir de la valeur C = 1 bit à mesure que l'amplitude efficace s du bruit est augmentée à partir de zéro. Par contre, quand q > 1, une entrée X = 1 (respectivement X = -1) est, à elle seule, incapable de déclencher une sortie Y = 1 (respectivement Y = -1). En l'absence du bruit, la capacité du canal est alors C = 0, le canal est incapable de transmettre aucune information. C'est l'ajout de bruit qui va permettre de transmettre de l'information sur le canal. L'ajout du bruit N rend possible un effet coopératif, dans lequel le bruit et l'entrée X collaborent pour atteindre le seuil qui contrôle le déclenchement de la sortie. Ceci se traduit par l'obtention d'une capacité C non nulle pour le canal, avec un domaine où C peut être augmentée grâce à une augmentation de l'amplitude efficace s du bruit. Puis lorsque le bruit devient trop fort, l'effet coopératif favorisant le signal cesse, et c'est le bruit essentiellement qui domine dans la sortie, conduisant à une capacité C qui se dégrade. Il existe donc, comme le montre la Fig. 4, une valeur optimale de l'amplitude efficace s du bruit pour laquelle la capacité C atteint un maximum, lequel dépend de la valeur de q > 1.

Fig. 4 : Capacité informationnelle
C (en bits) en fonction de l'amplitude efficace s
du bruit N gaussien centré ; les 9 courbes sont obtenues pour 9
valeurs du seuil q,
avec successivement de la courbe la plus haute à la plus basse :
q
= 0.8, 0.9, 0.95, 0.99, 1, 1.01, 1.05, 1.1, 1.2.
Un intérêt du présent exemple est d'illustrer le phénomène de résonance stochastique dans la transmission d'un signal apériodique porteur d'information, sur un modèle suffisamment simple pour être complètement calculable. Ce genre de modèle exactement calculable est rare dans le contexte non linéaire de la résonance stochastique.
D'un point de vue pratique,
si l'on dispose d'un contrôle complet sur l'amplitude du signal utile
ou sur le seuil
q
du système de transmission, il est plus avantageux, comme le montre
la Fig. 2, de fonctionner avec une amplitude du signal utile supérieure
au seuil
q.
Néanmoins, il existe des systèmes où ce type de contrôle
n'est pas disponible. C'est le cas par exemple pour une classe importante
de systèmes naturels réalisant du traitement de l'information
très performant : les systèmes neuronaux. Les neurones doivent
opérer sur des signaux, d'amplitude pouvant être arbitrairement
faible à leur limite de sensibilité, en présence d'un
seuil neuronal fixe.
4 Résonance stochastique chez les neurones
Il a été établi que la résonance stochastique opère dans la transmission des signaux par les neurones, à la fois sur des modèles théoriques , et de façon expérimentale. Ces études se sont concentrées sur le cas des neurones sensoriels périphériques, qui transmettent des signaux analogiques continus donnant l'image directe d'une grandeur de l'environnement. Nous avons montré la possibilité d'étendre la résonance stochastique aux neurones centraux, qui transmettent les signaux codés sous forme de trains d'impulsions stéréotypées, les potentiels d'action .
Pour illustration, nous allons présenter un mécanisme possible à l'aide d'un modèle simple qui décrit la non-linéarité essentielle lors de la transmission de trains de potentiels d'action par un neurone (intégration capacitive suivie d'une réponse à seuil). La membrane du neurone, de constante de temps tm, possède un potentiel électrique V(t) gouverné par
|
(21) |
Comme signaux d'entrée sur V(t) figure une composante cohérente s(t) = ånd(t-nTs) avec n entier, qui représente un train d'impulsions périodique de période Ts. De tels trains périodiques peuvent coder l'intensité d'un stimulus via leur période de décharge, et transportent ainsi de l'information utile. Dans d'autres circonstances, au sein des systèmes neuronaux, certains trains de potentiels d'action aussi peuvent être des signaux de bruit résultant de processus stochastiques neuronaux. Dans l'Eq. (21), un tel train de bruit est représenté par l'entrée h(t) = åkd(t-tk), où les tk sont des instants aléatoires poissonniens de densité 1/Th, de fonction d'autocorrélation Rhh(t) ºáh(t)h(t+t) ñ = D d(t)+D2, et de densité spectrale de puissance Phh(n) = D2 d(n)+D, avec D = 1/Th. Le paramètre w de l'Eq. (21) est un couplage synaptique, qui modélise l'efficacité des entrées, et qui pourrait être différent pour les voies cohérente et de bruit, mais que nous supposons identique ici pour limiter le nombre de paramètres.
Si le potentiel de membrane V atteint un seuil fixé VS > 0, un potentiel d'action est émis en sortie du neurone, puis V est remis à zéro, d'où les variations de V reprennent selon l'éq. (21). Le signal y(t) en sortie du neurone est donc constitué par un train d'impulsions évoluant selon :
|
||||||||||||||
La réponse de l'éq. (21) à un unique potentiel d'action à t0 est, pour t > t0 :
|
(23) |
Pour quantifier cet effet, il est possible de calculer la fonction d'autocorrélation temporelle Ryy(t) ºáy(t)y(t+t) ñ du train de sortie, puis, par transformation de Fourier, sa densité spectrale de puissance Pyy(n). La corrélation du train de sortie y(t) avec l'entrée Ts-périodique s(t) se manifeste à nouveau sur Pyy(n) par des raies spectrales aux harmoniques n/Ts émergeant d'un fond continu de bruit. Un rapport signal sur bruit (RSB) en sortie peut alors être introduit comme dans l'Eq. (9). La Fig. 5 montre l'évolution du RSB de sortie, en fonction de la puissance du bruit d'entrée, obtenue lors d'une simulation du modèle de neurone. L'évolution résonnante du RSB, qui culmine pour une puissance optimale non nulle du bruit, signe la résonance stochastique.

Fig. 5 : Rapport signal sur bruit
en sortie, en fonction de la puissance du bruit en entrée D/(1/Ts),
à la fréquence fondamentale 1/Ts en (a), et aux
harmoniques 2/Ts en (b), et 4/Ts en (c).
Des modèles plus élaborés de neurone montrent la persistance de l'effet, ainsi que d'autres mécanismes pour utiliser le bruit au profit de l'information utile, y compris en présence de signaux cohérents apériodiques.
Conclusion
La résonance stochastique,
entendue comme un effet de transmission non linéaire du signal assistée
par le bruit, et sa généralisation sous diverses formes à
différents types de signaux et systèmes, constituent des
avancées relativement récentes. Actuellement, la pertinence
et l'intérêt de la résonance stochastique se disposent
le long de trois directions principales :
1. La résonance stochastique
présente un intérêt conceptuel important, en ce qu'elle
illustre, de manière précise et quantifiée, la possibilité,
dans des systèmes complexes (non linéaires), d'extraire de
l'ordre hors du désordre ou du signal utile hors du bruit. Jusqu'à
présent, c'est plutôt cet aspect conceptuel qui a été
approfondi.
2. Il a été
établi par des travaux nombreux, que la résonance stochastique
opère dans une classe importante de systèmes naturels très
efficaces pour le traitement de l'information : les systèmes neuronaux.
La résonance stochastique peut donc être étudiée
comme une propriété signifiante pour le traitement non linéaire
du signal par les neurones.
3. Une troisième
voie d'intérêt est constituée par les applications
technologiques de la résonance stochastique. Cette question commence
tout juste à être abordée, et demeure encore largement
à explorer. Des possibilités sont envisagées pour
la détection de faibles signaux bruités, dans certains dispositifs
. Les potentialités révélées par la résonance
stochastique rendent de telles explorations très valables.
Des développements spécialement féconds pourraient survenir en examinant en même temps les directions 2 et 3 précédentes. Une limitation dans les applications technologiques est que la résonance stochastique est essentiellement un effet non linéaire, opérant principalement en présence de non-linéarités à seuil ou dans des systèmes dont les états accessibles sont séparés par des barrières de potentiel. Par opposition, dans les dispositifs technologiques conçus pour l'acquisition et le traitement du signal, spécialement aux bas niveaux de traitement là où le bruit ambiant peut être important, l'effort vise principalement à rendre linéaires les systèmes, interdisant ainsi l'exploitation de la résonance stochastique. Les traitements linéaires présentent de nombreux avantages, spécialement dans la conception et le contrôle de dispositifs technologiques ; ils présentent également des limitations. De leur côté, les systèmes neuronaux naturels offrent l'exemple de systèmes très performants pour le traitement de l'information, qui mettent en jeu, dès les plus bas niveaux, des constituants intrinsèquement non linéaires. On peut voir là la suggestion de possibilités radicalement distinctes, encore à élucider, pour un traitement de l'information essentiellement non linéaire, où la résonance stochastique serait une propriété parmi d'autres concourant à l'efficacité des performances.
File translated from TEX
by TTH, version
2.20. (qui n'a pas réussi a traduire les références
pour l'instant...)